بحث عن متوازي الاضلاع

جميع زواياه الأربعة قوائم.

بحث عن متوازي الاضلاع. 1 2 3 وفي الهندسة الإقليدية تكون جميع زوايا المثلث المتساوي الأضلاع متساوية القياس وقياس كل منهما 60. هناك ثلاثة حالات خاصة من متوازي الاضلاع وهي المستطيل والمعين والمربع وفيما يلي توضيح لكل منها. Equilateral triangle هو مثلث جميع أضلاعه متساوية الطول. في الهندسة الرياضية المثلث المتساوي الأضلاع بالإنجليزية.

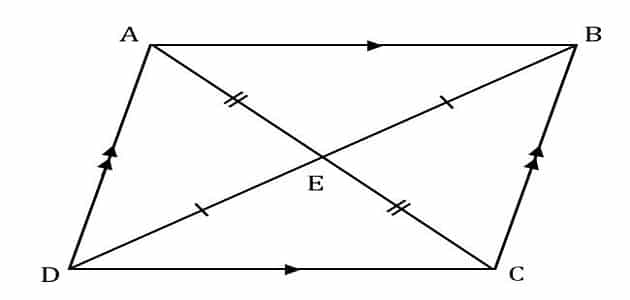
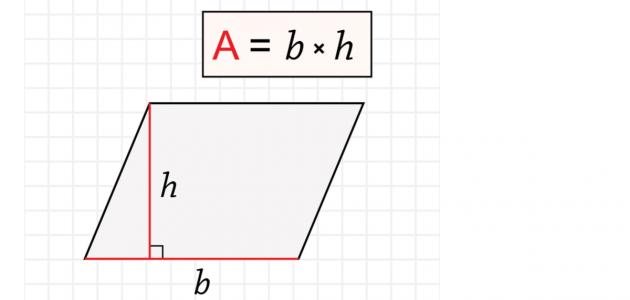
يمكن تعريف قطري متوازي الاضلاع بأن هما الخطان المستقيمان الواصلان بين كل زاويتين متقابلتين فيه أما عن طولهما فيمكن قياسه باستخدام القانون الآتي. هو شكل هندسي رباعي مجموع زواياه 360 درجة فيه كل ضلعين متقابلين متوازيين فمثلا إذا نظرنا إلى الشكل المقابل سنجد أن الضلع ab يوازي الضلع المقابل له dc والضلع da يوازي الضلع المقابل له cb كما نلاحظ أن أى مستقيم يمر بمركز متوازي الأضلاع يقوم. طول القطر ق ل الجذر التربيعي أ2 ب2 2 أ ب جتا أ. ومتوازي الأضلاع هو أحد الأشكال الثنائية الأبعاد ويتم رسمه في مستويات ديكارتيه على محاور سينيه وصادية وكل الأشكال الثنائية لها مساحة خاصة بها وقد تم عمل مساحة متوازي الأضلاع من خلال المساحات للمثلث والمستطيل لأن متوازي الأضلاع إذا تمت تجزئته سوف نحصل على مستطيل ومثلث.

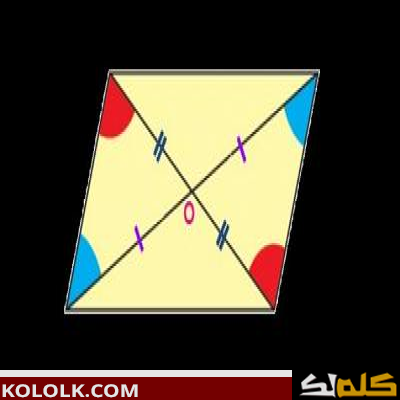
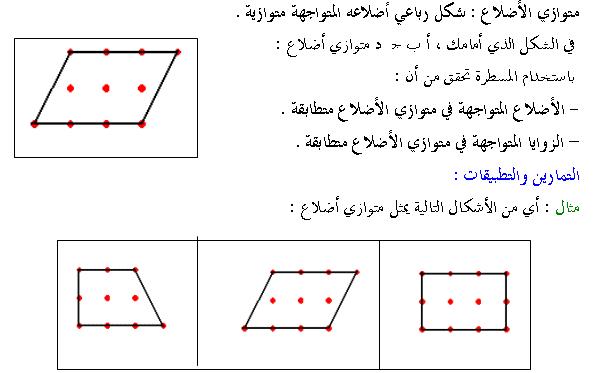
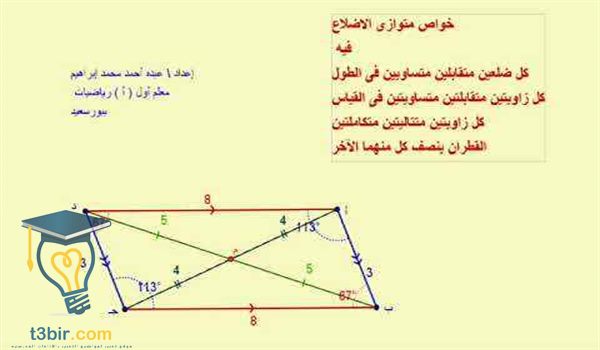
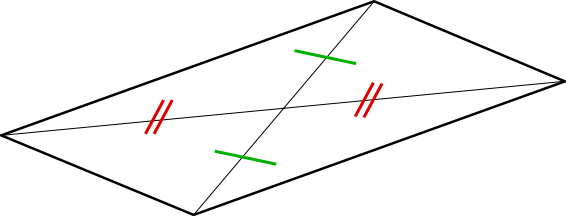
مساحة متوازي الأضلاع تساوي ضعف مساحة المثلث المشكل بضلعين وقطر. أما القانون الذي يربط بين طول أضلاع متوازي الأضلاع وبين طول أقطاره فهو. كل قطر في متوازي الأضلاع منصف للقطر الآخر. متوازي الأضلاع فى الرياضيات هو شكل رباعي ثنائي الأبعاد كل ضلعين متقابلين فيه متساويين في الطول ومتوازيين وكل زاويتين متقابلتين متساويتين ويقسمه قطراه إلى نصفين متساويين.

يتقاطع قطراه في نقطة تشكل مركز تناظر لمتوازي الأضلاع وتسمى مركز متوازي الأضلاع. محيط متوازي الأضلاع مجموع أطوال أضلاعه او ضعف مجموع طولي ضلعين متجاورين. بحث في هذا. بحث عن متوازي الاضلاع.